3.7. Parallel Query
Parallel Query, supported from version 9.6, is a feature that processes a single query using multiple processes (Workers).
For instance, if certain conditions are met, the PostgreSQL process that executes the query becomes the Leader and starts up to Worker processes (maximum number is max_parallel_workers_per_gather). Each Worker process then performs scan processing, and returns the results sequentially to the Leader process. The Leader process aggregates the results returned from the Worker processes.
Figure 3.38 illustrates how a sequential scan query is processed by two Worker processes.
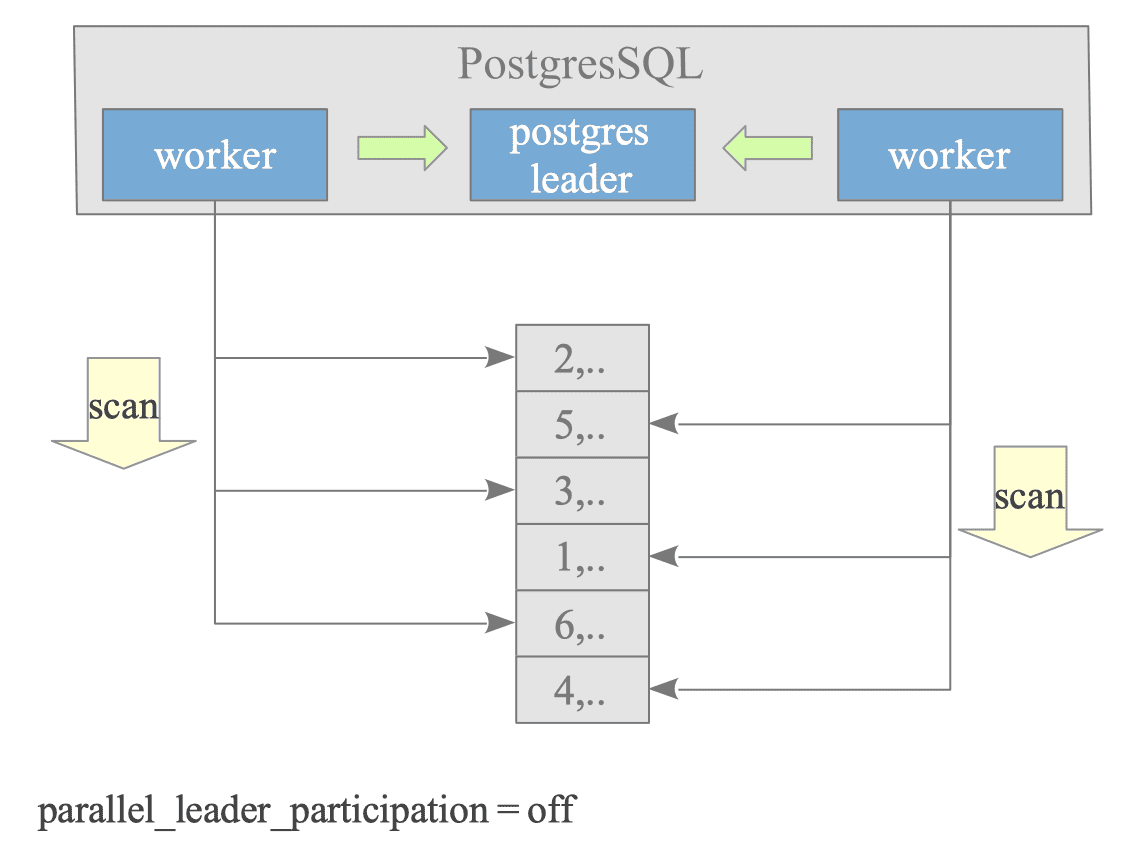
Figure 3.38. Parallel Query Concept.
The configuration parameter parallel_leader_participation, introduced in version 14, allows the Leader process to also process queries while waiting for responses from Workers. The default is on.
However, to simplify the explanation and diagrams, we will explain this under the assumption that the Leader process does not process queries (i.e., parallel_leader_participation is off).
Parallel Query is gradually improved. Table 3.2 highlights key points from the official documentation’s release notes about Parallel Query.
| Version | Description |
|---|---|
| 9.6 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 14 |
|
| 15 |
|
| 16 |
|
Note that Parallel Query is primarily READ-ONLY and does not yet support cursor operations.
In the following, we will first provide an overview of Parallel Query, then explore Join operations, and finally explain how aggregate functions are calculated in parallel queries.
3.7.1. Overview
Figure 3.39 briefly describes how parallel query performs in PostgreSQL.
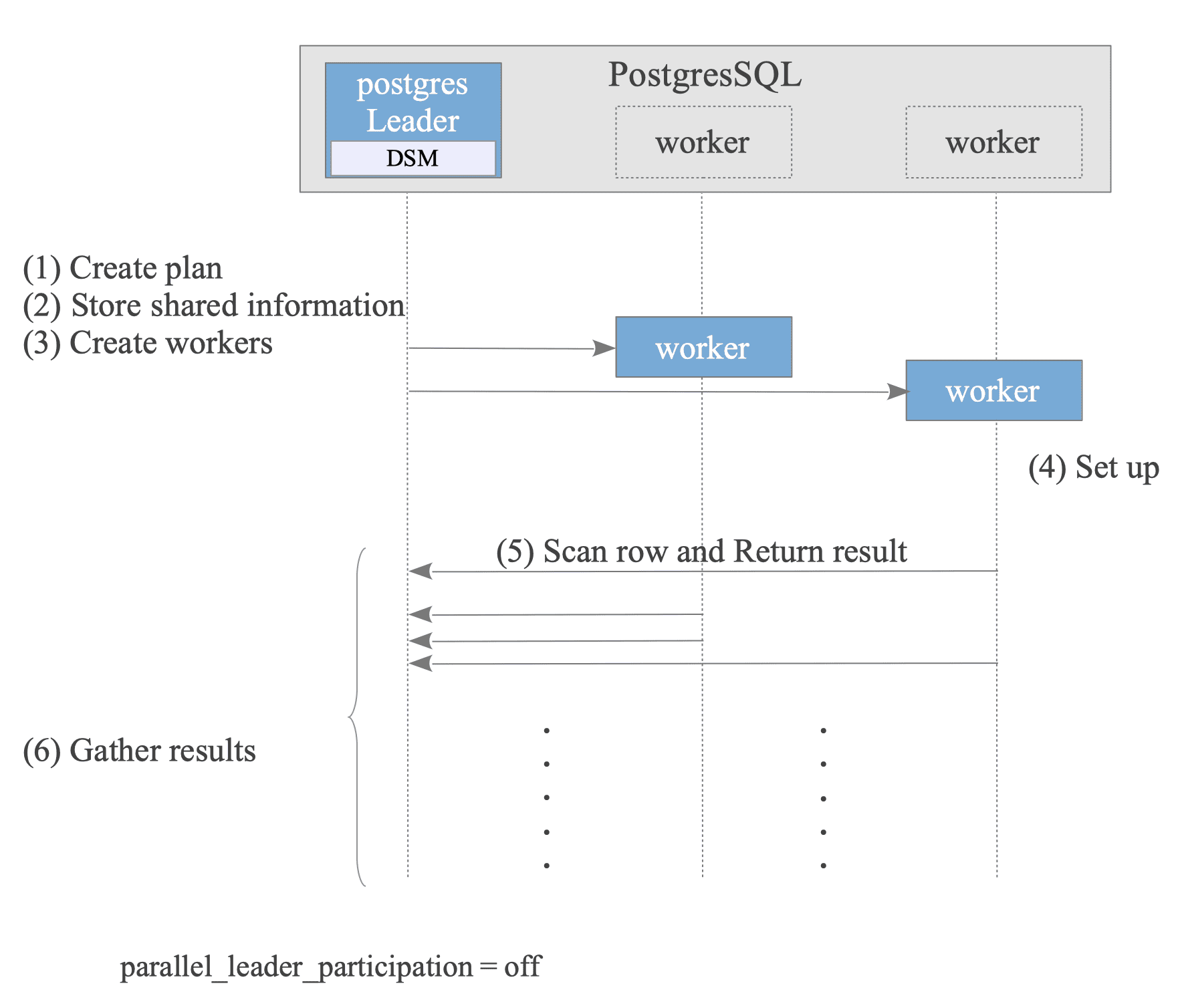
Figure 3.39. How Parallel Query Performs.
- Leader Creates Plan:
The optimizer creates a plan that can be executed in parallel. - Leader Stores Shared information:
To execute the plan on both the Leader and Worker nodes, the Leader stores necessary information in its Dynamic Shared Memory (DSM) area. For more details, see the following explanation. - Leader Creates Workers.
- Worker Sets up State:
Each worker reads the stored shared information to sets up its state, ensuring a consistent execution environment with the Leader. - Worker Scans rows and Returns results.
- Leader Gathers results.
- After the query finishes, the Workers are terminated, and the Leader releases the DSM area.
In Parallel Query processing, the Leader and Worker processes communicate Dynamic Shared Memory (DSM) area.
The Leader process allocates memory space on demand (i.e., it can be allocated as needed and released when no longer required). Worker processes can then read and write data to these memory regions as if they were their own.
In this section,
to demonstrate using concrete examples, we use Table d as follows:
testdb=# CREATE TABLE d (id double precision, data int);
CREATE TABLE
testdb=# INSERT INTO d SELECT i::double precision, (random()*1000)::int FROM generate_series(1, 1000000) AS i;
INSERT 0 1000000
testdb=# ANALYZE;
ANALYZE3.7.1.1. Creating Parallel Plan
Parallel Query is not always considered. If the table size to be scanned is greater than or equal to min_parallel_table_scan_size (default is 8MB), or if the index size to be scanned is greater than or equal to min_parallel_index_scan_size (default is 512kB), the optimizer will consider Parallel Query.
Here is the simplest plan in parallel query:
|
|
As shown above, the simplest plan consists of a Gather node and a Seq Scan node.
Figure 3.40 shows the plan tree of the above query:
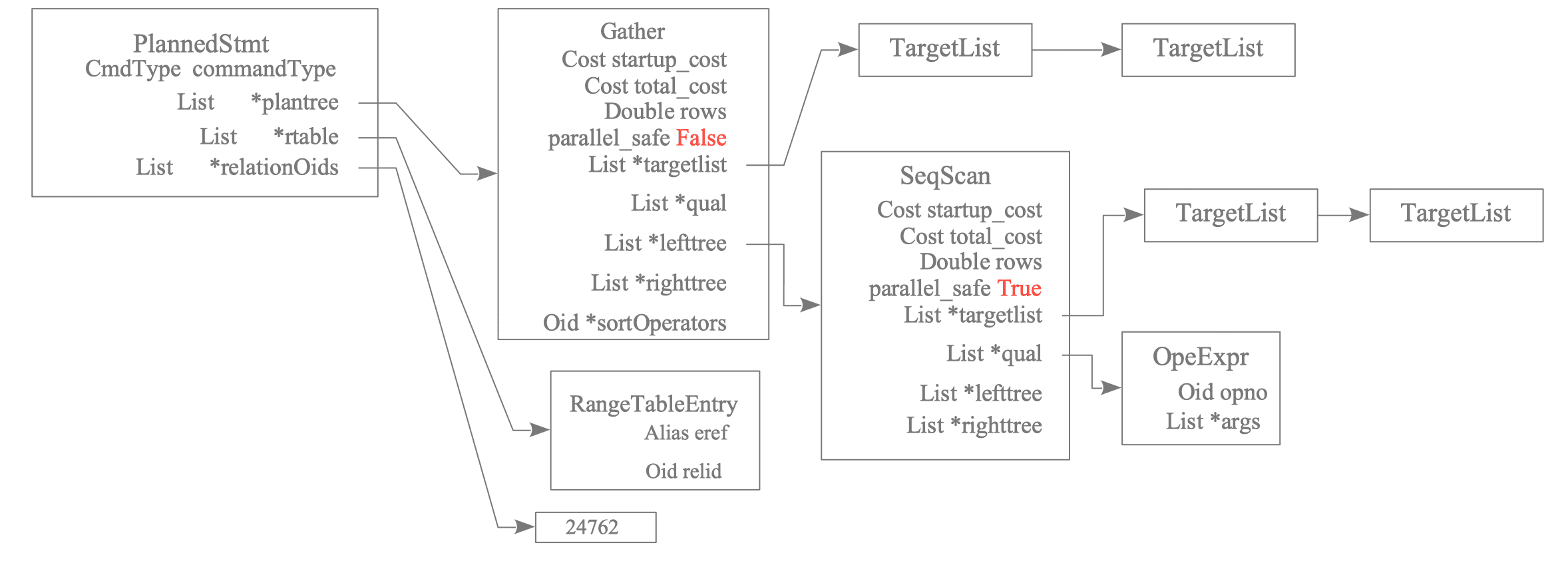
Figure 3.40. Leader's Plan Tree
The Gather node is specific to Parallel Query and collects the results from the Workers. In addition to Gather, Parallel Query has the following specific nodes:
- GatherMerge
- Append and AppendMerge (See Official Document.)
- Finalize/Partial Aggregate (See Section 3.7.3.)
The nodes executed by Workers are generally the subplan tree below the Gather node, and the parallel_safe value is set to True.
In the above example, the Seq Scan node and below, which is under the Gather node, are executed by Workers.
3.7.1.2. Storing Shared Information
To execute the query collaboratively with the Workers, the Leader stores information to be shared with the Workers in its DSM (Dynamic Shared Memory) area.
The Leader and Workers share two types of information: execution state and query.
-
Execution State:
The environment information necessary for the Leader and Workers to execute the same query consistently. See README.parallel in details. This includes information such as:- All configuration parameters (GUC)
- The transaction snapshot, the current subtransaction’s XID. (For more details on these, see Chapter 5.)
- The set of libraries dynamically loaded by dfmgr.c.
This information is stored by InitializeParallelDSM().
-
Query:
This includes information such as:- PlannedStmt
- ParamListInfo
- The Description structures of nodes executed by Worker. For example, the SeqScan node uses
ParallelTableScanDesc; the IndexScan node usesParallelIndexScanDesc. See ExecParallelInitializeDSM() for detail. - The instrumentation and usage information for reporting purposes.
This information is stored by ExecInitParallelPlan().
Additionally, the Leader creates a TupleQueue (based on tqueue.c) on DSM to read the Worker’s results.
3.7.1.3. Creating Workers
The number of Workers planned in the query plan may differ from the actual number of Workers running. This is because the maximum number of Workers is limited by max_parallel_workers, and there may not be enough available Workers due to other parallel query processes.
The EXPLAIN ANALYZE command shows both the planned and launched number of Workers.
testdb=# EXPLAIN ANALYZE SELECT * FROM d WHERE id BETWEEN 1 AND 100;
QUERY PLAN
------------------------------------------------------------------------------------------------------------------
Gather (cost=1000.00..16609.10 rows=1 width=12) (actual time=60.035..60.994 rows=100 loops=1)
Workers Planned: 2
Workers Launched: 2
-> Parallel Seq Scan on d (cost=0.00..15609.00 rows=1 width=12) (actual time=31.073..52.248 rows=50 loops=2)
Filter: ((id >= '1'::double precision) AND (id <= '100'::double precision))
Rows Removed by Filter: 499950
Planning Time: 0.265 ms
Execution Time: 61.012 ms
(8 rows)3.7.1.4. Setting Up Workers
Upon startup, a Worker reads the shared Execution State and Query information prepared by the Leader.
By setting the Execution State information, the Worker can execute the query in the same environment as the Leader.
When reading the Query information, the ExecSerializePlan() function is used to generate and save a plan tree for the Worker based on the PlannedStmt. Specifically, a new sub-plan tree (typically a Gather node sub-plan tree) where parallel_safe is True is generated as the Worker’s plan tree.
Figure 3.41 shows the plan tree of the Worker.
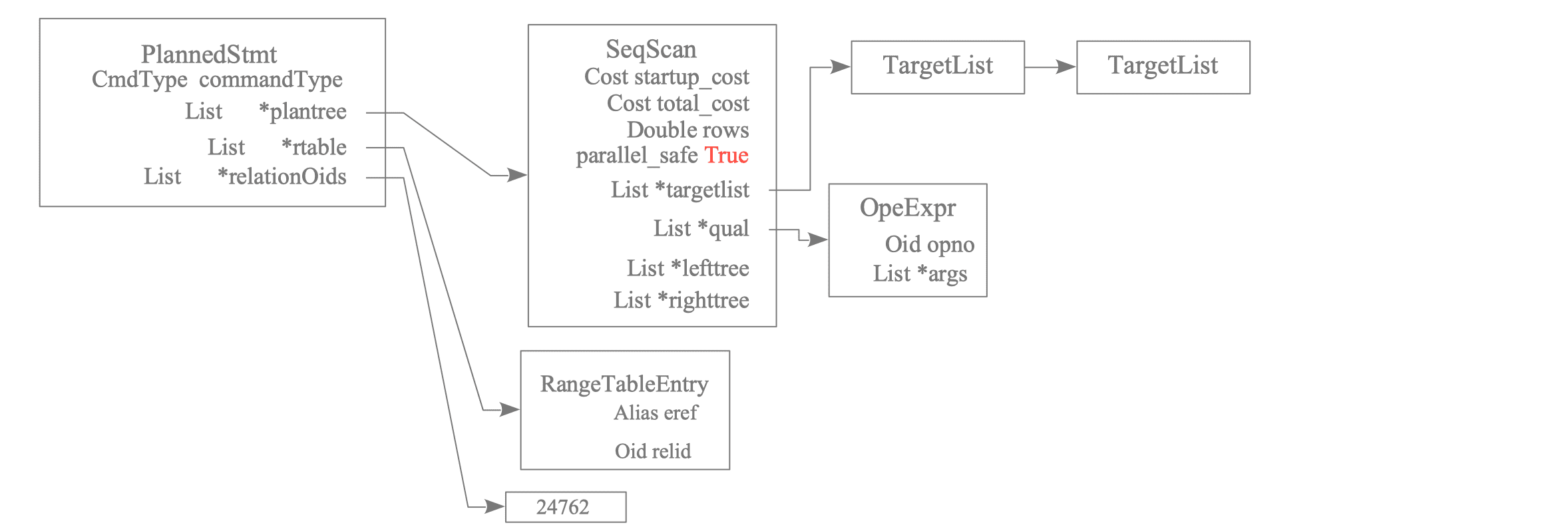
Figure 3.41. Worker's Plan Tree Generated from Leader's Plan Tree
3.7.1.5. Scanning Rows and Returning Results
As discussed in Section 3.4.1.1, the Executor’s methods for accessing individual data tuples are highly abstracted. This principle extends to Parallel Queries.
Although a detailed explanation is omitted, since the Leader and Workers share the query execution environment via DSM, a single sequential scan can be executed in parallel by the Leader and Workers calling the SeqNext() function.
Similarly, results are returned to the Gather node via a TupleQueue on DSM.
3.7.1.6. Gathering Results
The Gather node, a Parallel Query specific node, gathers the results returned by the Workers.
3.7.2. Parallel Join
Parallel Query in PostgreSQL supports nested-loop joins, merge joins, and hash joins.
In this section, we will use the following tables: d and f:
testdb=# CREATE TABLE d (id double precision, data int);
CREATE TABLE
testdb=# INSERT INTO d SELECT i::double precision, (random()*1000)::int FROM generate_series(1, 1000000) AS i;
INSERT 0 1000000
testdb=# CREATE INDEX d_id_idx ON d (id);
CREATE INDEX
testdb=# CREATE TABLE f (id double precision, data int);
CREATE TABLE
testdb=# INSERT INTO f SELECT i::double precision, (random()*1000)::int FROM generate_series(1, 10000000) AS i;
INSERT 0 10000000
testdb=# \d d
Table "public.d"
Column | Type | Collation | Nullable | Default
--------+------------------+-----------+----------+---------
id | double precision | | |
data | integer | | |
Indexes:
"d_id_idx" btree (id)
testdb=# \d f
Table "public.f"
Column | Type | Collation | Nullable | Default
--------+------------------+-----------+----------+---------
id | double precision | | |
data | integer | | |
testdb=# ANALYZE;
ANALYZE3.7.2.1. Nested Loop Join
In a nested loop join, the inner table is always processed for all rows, not in parallel.
Therefore, for example, in a materialized nested loop join, each Worker must materialize the inner table independently, which is inefficient.
testdb=# SET enable_nestloop = ON;
SET
testdb=# SET enable_mergejoin = OFF;
SET
testdb=# SET enable_hashjoin = OFF;
SET
testdb=# EXPLAIN SELECT * FROM d, f WHERE d.data = f.data AND f.id < 10000;
QUERY PLAN
-------------------------------------------------------------------------------
Gather (cost=1000.00..97163469.29 rows=9651513 width=24)
Workers Planned: 2
-> Nested Loop (cost=0.00..96197317.99 rows=4825756 width=24)
Join Filter: (d.data = f.data)
-> Parallel Seq Scan on f (cost=0.00..121935.99 rows=4831 width=12)
Filter: (id < '10000'::double precision)
-> Materialize (cost=0.00..27992.00 rows=1000000 width=12)
-> Seq Scan on d (cost=0.00..18109.00 rows=1000000 width=12)
(8 rows)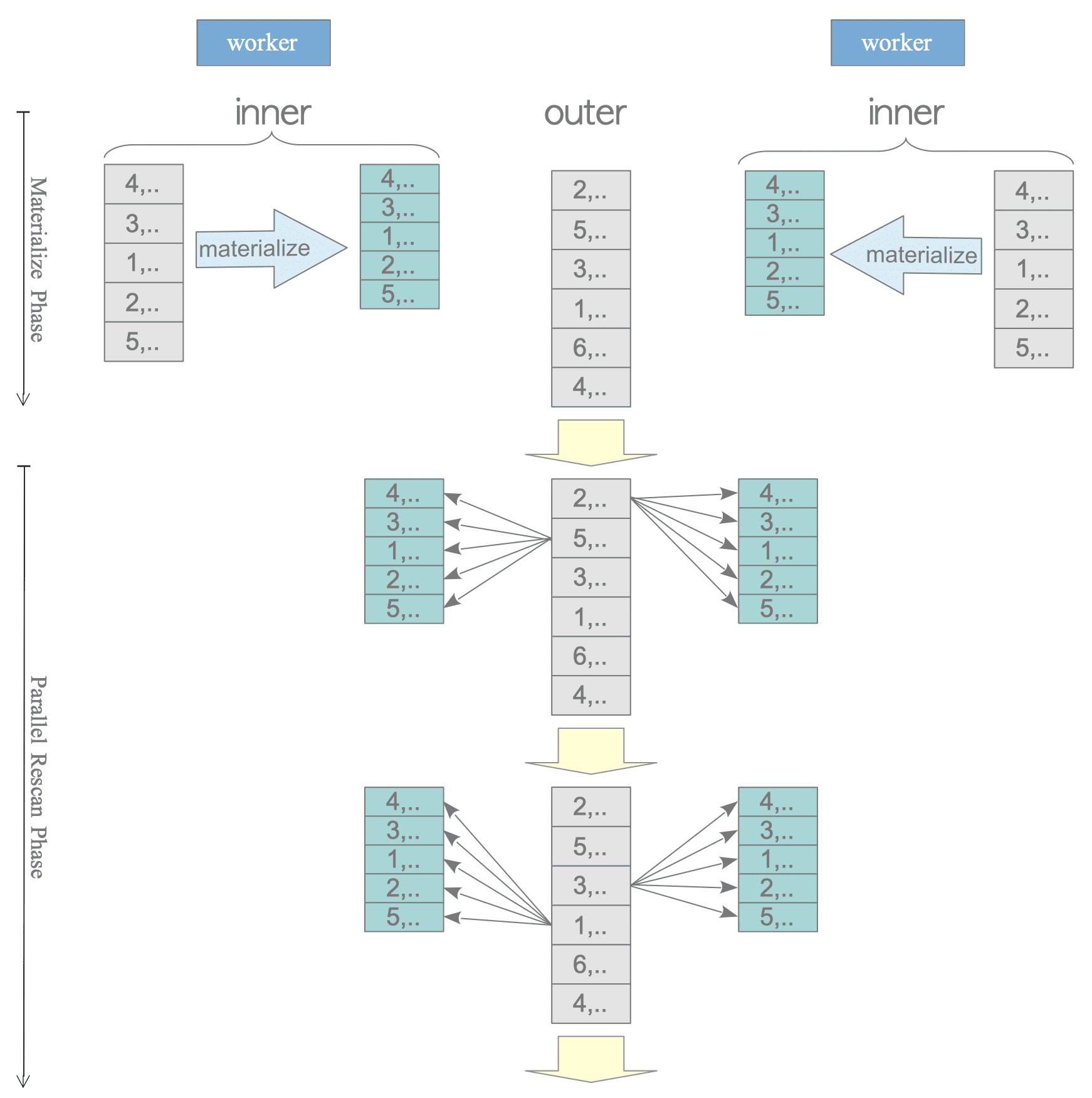
Figure 3.42. Materialize Nested Loop Join in Parallel Query.
On the other hand, in an Indexed Nested Loop Join, the inner table can be scanned in parallel by the Workers, making it more efficient.
testdb=# EXPLAIN SELECT * FROM d, f WHERE d.id = f.id AND f.id < 10000;
QUERY PLAN
-------------------------------------------------------------------------------
Gather (cost=1000.42..142818.71 rows=967 width=24)
Workers Planned: 2
-> Nested Loop (cost=0.42..141722.01 rows=484 width=24)
-> Parallel Seq Scan on f (cost=0.00..121935.99 rows=4831 width=12)
Filter: (id < '10000'::double precision)
-> Index Scan using d_id_idx on d (cost=0.42..4.09 rows=1 width=12)
Index Cond: (id = f.id)
(7 rows)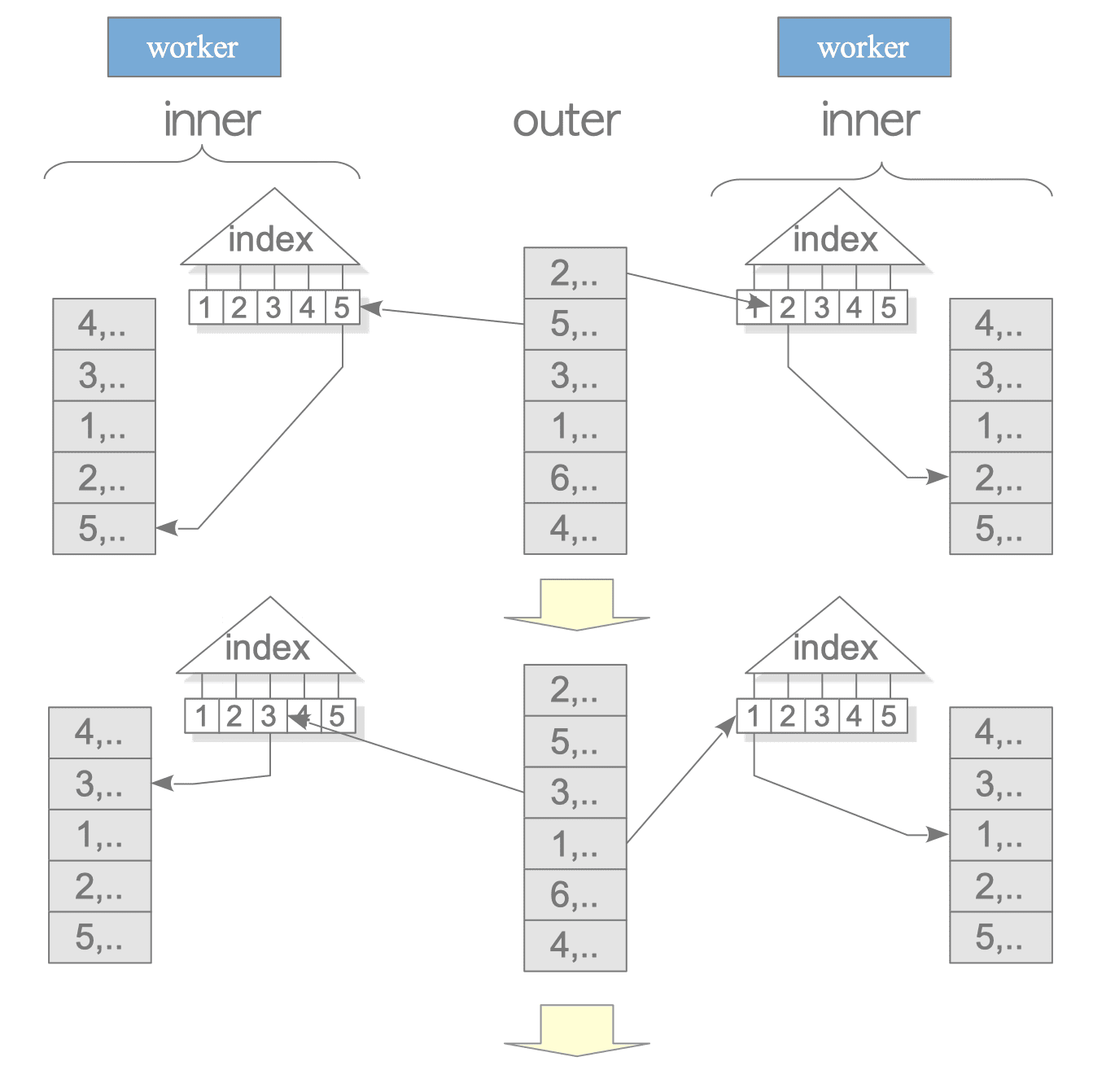
Figure 3.43. Indexed Nested Loop Join in Parallel Query.
3.7.2.2. Merge Join
Like nested loop joins, a merge join always processes the inner table for all rows, not in parallel. Therefore, each Worker performs the sorting process of the inner table independently.
However, if the inner table is accessed using an index scan, the join operation can be performed efficiently, similar to an Indexed Nested Loop Join.
testdb=# SET enable_nestloop = OFF;
SET
testdb=# SET enable_mergejoin = ON;
SET
testdb=# SET enable_hashjoin = OFF;
SET
testdb=# EXPLAIN SELECT * FROM d, f WHERE d.id = f.id AND d.id < 100000;
QUERY PLAN
----------------------------------------------------------------------------------------
Gather (cost=837387.83..853944.33 rows=97361 width=24)
Workers Planned: 2
-> Merge Join (cost=836387.83..843208.23 rows=48680 width=24)
Merge Cond: (f.id = d.id)
-> Sort (cost=836385.61..848880.80 rows=4998079 width=12)
Sort Key: f.id
-> Parallel Seq Scan on f (cost=0.00..109440.79 rows=4998079 width=12)
-> Index Scan using d_id_idx on d (cost=0.42..3569.24 rows=97361 width=12)
Index Cond: (id < '100000'::double precision)
(9 rows)3.7.2.3. Hash Join
In versions 10 and 9.6, during a Parallel Query Hash Join, each Worker performs the hash table build process for the inner table independently.
testdb=# SET enable_nestloop = OFF;
SET
testdb=# SET enable_mergejoin = OFF;
SET
testdb=# SET enable_hashjoin = ON;
SET
testdb=# SET enable_parallel_hash = OFF;
SET
testdb=# EXPLAIN SELECT * FROM d, f WHERE d.id = f.id;
QUERY PLAN
----------------------------------------------------------------------------------
Gather (cost=36492.00..323368.59 rows=1000000 width=24)
Workers Planned: 2
-> Hash Join (cost=35492.00..222368.59 rows=500000 width=24)
Hash Cond: (f.id = d.id)
-> Parallel Seq Scan on f (cost=0.00..109440.79 rows=4998079 width=12)
-> Hash (cost=18109.00..18109.00 rows=1000000 width=12)
-> Seq Scan on d (cost=0.00..18109.00 rows=1000000 width=12)
(7 rows)Parallel hash join was supported in version 11 (enable_parallel_hash, enabled by default). With this feature, hash tables are created for each Worker during the build phase and are shared between workers, making the build phase more efficient.
testdb=# SET enable_parallel_hash = ON;
SET
testdb=# EXPLAIN SELECT * FROM d, f WHERE d.id = f.id;
QUERY PLAN
--------------------------------------------------------------------------------------
Gather (cost=22801.00..304736.59 rows=1000000 width=24)
Workers Planned: 2
-> Parallel Hash Join (cost=21801.00..203736.59 rows=500000 width=24)
Hash Cond: (f.id = d.id)
-> Parallel Seq Scan on f (cost=0.00..109440.79 rows=4998079 width=12)
-> Parallel Hash (cost=13109.00..13109.00 rows=500000 width=12)
-> Parallel Seq Scan on d (cost=0.00..13109.00 rows=500000 width=12)
(7 rows)3.7.3. Parallel Aggregate
Almost aggregate functions in PostgreSQL can be also processed in parallel.
Whether an aggregate function can be parallelized depends on whether Partial Mode is set to YES
in Official Document.
When the predicted number of target rows is small:
- Scanned rows from each Worker, processed by the parallel (seq) scan node, are gathered at the gather node.
- These gathered rows are then aggregated at the aggregate node.
See the following examples:
testdb=# EXPLAIN SELECT avg(id) FROM d where id BETWEEN 1 AND 10;
QUERY PLAN
------------------------------------------------------------------------------------------
Aggregate (cost=16609.10..16609.11 rows=1 width=8)
-> Gather (cost=1000.00..16609.10 rows=1 width=8)
Workers Planned: 2
-> Parallel Seq Scan on d (cost=0.00..15609.00 rows=1 width=8)
Filter: ((id >= '1'::double precision) AND (id <= '10'::double precision))
(5 rows)
testdb=# EXPLAIN SELECT var_pop(id) FROM d where id BETWEEN 1 AND 10;
QUERY PLAN
------------------------------------------------------------------------------------------
Aggregate (cost=16609.10..16609.11 rows=1 width=8)
-> Gather (cost=1000.00..16609.10 rows=1 width=8)
Workers Planned: 2
-> Parallel Seq Scan on d (cost=0.00..15609.00 rows=1 width=8)
Filter: ((id >= '1'::double precision) AND (id <= '10'::double precision))
(5 rows)When the predicted number of target rows is large:
- Scanned rows from each Worker, processed by the parallel sequential scan node, are partially aggregated at the aggregate node.
- These intermediate aggregated results are gathered at the gather node.
- They are then finally aggregated at the finalize aggregate node.
See the following examples:
testdb=# EXPLAIN SELECT avg(id) FROM d where data > 100;
QUERY PLAN
-------------------------------------------------------------------------------------
Finalize Aggregate (cost=16485.14..16485.15 rows=1 width=8)
-> Gather (cost=16484.93..16485.14 rows=2 width=32)
Workers Planned: 2
-> Partial Aggregate (cost=15484.93..15484.94 rows=1 width=32)
-> Parallel Seq Scan on d (cost=0.00..14359.00 rows=450371 width=8)
Filter: (data > 100)
(6 rows)
testdb=# EXPLAIN SELECT var_pop(id) FROM d where data > 100;
QUERY PLAN
-------------------------------------------------------------------------------------
Finalize Aggregate (cost=16485.14..16485.15 rows=1 width=8)
-> Gather (cost=16484.93..16485.14 rows=2 width=32)
Workers Planned: 2
-> Partial Aggregate (cost=15484.93..15484.94 rows=1 width=32)
-> Parallel Seq Scan on d (cost=0.00..14359.00 rows=450371 width=8)
Filter: (data > 100)
(6 rows)Multiple sums, averages, and variances can be calculated using the following formulas:
$$ \begin{align} S_{n} &= S_{n_{1}} + S_{n_{2}} \\ A_{n} &= \frac{1}{n_{1} + n_{2}} (S_{n_{1}} + S_{n_{2}} ) \\ V_{n} &= (V_{n_{1}} + V_{n_{2}}) + \frac{n_{1} n_{2}}{n_{1} + n_{2}} \left(\frac{S_{n_{1}}}{n_{1}} - \frac{S_{n_{2}}}{n_{2}} \right)^{2} \end{align} $$The finalize aggregate node aggregates the intermediate results using the formulas above.
For three or more values, the process can be repeated iteratively, adding one value at a time.
Given:
- A dataset: $ \{ x_{i} | 1 \le i \le n = n_{1} + n_{2} \} $
- The overall average: $A_{n} = \sum_{i=1}^{n_{1}+n_{2}} x_{i}$
- The sum of the first part of the dataset: $S_{n_{1}} = \sum_{i=1}^{n_{1}} x_{i}$
- The variance of the first part: $V_{n_{1}} = \sum_{i=1}^{n_{1}} (x_{i} - \frac{S_{n_{1}}}{n_{1}})^{2}$
- The sum of the second part of the dataset: $S_{n_{2}} = \sum_{i=1+n_{1}}^{n_{1}+n_{2}} x_{i}$
- The variance of the second part: $V_{n_{2}} = \sum_{i=1+n_{1}}^{n_{1}+n_{2}} (x_{i} - \frac{S_{n_{2}}}{n_{2}})^{2}$
To Prove:
The variance of the entire dataset, $V_{n}$, can be expressed in terms of $V_{n_{1}}$, $V_{n_{2}}$, $S_{n_{1}}$, and $S_{n_{2}}$ as follows:
$$ V_{n} = V_{n_{1}} + V_{n_{2}} + \frac{n_{1} n_{2}}{n_{1} + n_{2}} \left( \frac{S_{n_{1}}}{n_{1}} - \frac{S_{n_{2}}}{n_{2}} \right)^{2} $$