2.1. Formulation of Neural Networks
The formulation of the one-hidden layer neural network is defined as follows:
$$ \begin{cases} \hat{h} = W x + b \\ h = f(\hat{h}) \\ \hat{y} = U h + c \\ y = g(\hat{y}) \end{cases} \tag{2.1} $$Given that the number of input nodes, hidden nodes, and output nodes are $i, h $, and $o$, respectively, then:
- $x \in \mathbb{R}^{i} $ is an input vector.
- $W \in \mathbb{R}^{h \times i} $ is the weight matrix for the hidden layer.
- $b \in \mathbb{R}^{h} $ is the bias term for the hidden layer.
- $h \in \mathbb{R}^{h} $ is the output of the hidden layer.
- $U \in \mathbb{R}^{o \times h} $ is the weight matrix for the output layer.
- $c \in \mathbb{R}^{o} $ is the bias term for the output layer.
- $y \in \mathbb{R}^{o} $ is the output vector.
- $f(\cdot)$ and $g(\cdot)$ are activation functions.
In this chapter, we will explore a network with $i = 2$, $h = 3$ and $o = 1$, employing the sigmoid function $\sigma(\cdot)$ as the activation function. The formulation in $(2.1)$ can then be explicitly written as:
$$ \begin{align} \begin{pmatrix} \hat{h_{0}} \\ \hat{h_{1}} \\ \hat{h_{2}} \end{pmatrix} &= \begin{pmatrix} W_{00} & W_{01} \\ W_{10} & W_{11} \\ W_{20} & W_{21} \end{pmatrix} \begin{pmatrix} x_{0} \\ x_{1} \end{pmatrix} + \begin{pmatrix} b_{0} \\ b_{1} \\ b_{2} \end{pmatrix} \\ \begin{pmatrix} h_{0} \\ h_{1} \\ h_{2} \end{pmatrix} &= \begin{pmatrix} \sigma(\hat{h_{0}}) \\ \sigma(\hat{h_{1}}) \\ \sigma(\hat{h_{2}}) \end{pmatrix} \\ \hat{y} &= \begin{pmatrix} U_{00} & U_{01} & U_{02} \end{pmatrix} \begin{pmatrix} h_{0} \\ h_{1} \\ h_{2} \end{pmatrix} + c \\ y &= \sigma(\hat{y}) \end{align} $$Fig.2-1 illustrates this neural network’s structure:
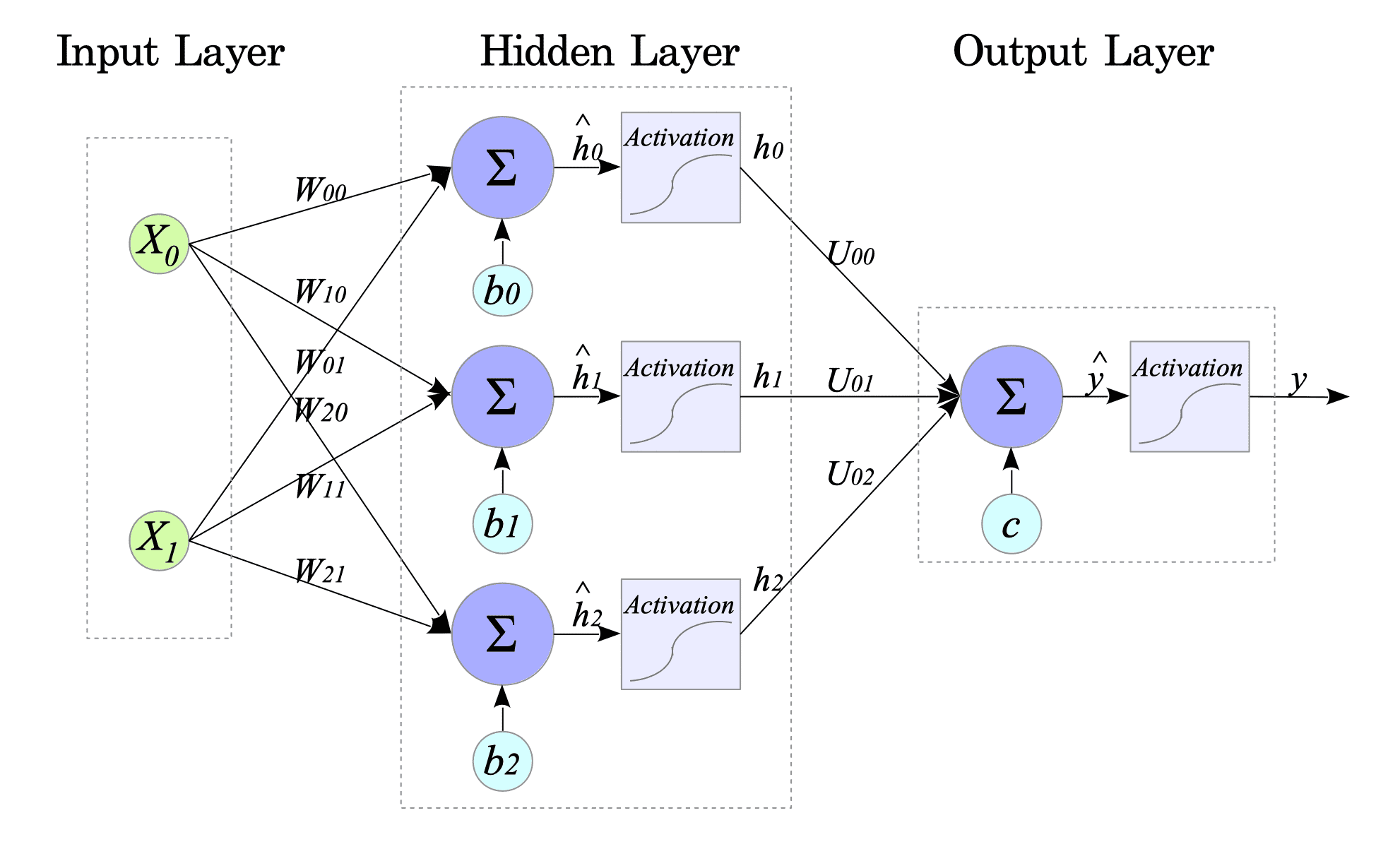
Fig.2-1: Neural Network Architecture
The network contains the unknown parameters $W$, $U$, $b$ and $c$. Their sizes are:
$$ \begin{align} |W| &= | \text{input_nodes} | \times | \text{hidden_nodes} | = 2 \times 3 = 6 \\ |U| &= | \text{hidden_nodes} | \times | \text{output_nodes} | = 3 \times 1 = 3 \\ |b| &= | \text{hidden_nodes} | = 3 \\ |c| &= 1 \end{align} $$In total, 13 parameters ($6 + 3 + 3 + 1$) should be determined through training.