8.3. Implementation
Complete Python code is available at: LSTM_from_scrtch.py
The LSTM class is shown below:
class LSTM:
def __init__(self, input_units, hidden_units, return_sequences=False):
self.return_sequences = return_sequences
self.input_units = input_units
self.hidden_units = hidden_units
"""
Initialize random weights and bias using Glorot
and Orthogonal Weight Initializations.
Glorat Weight Initialization: Glorot & Bengio, AISTATS 2010
http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
Orthogonal Weight Initialization: Saxe et al.,
https://arxiv.org/pdf/1312.6120.pdf
"""
self.Wi = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.Wf = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.Wc = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.Wo = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.Ui = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.Ui, _, _ = np.linalg.svd(self.Ui) # Orthogonal Weight Initialization
self.Uf = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.Uf, _, _ = np.linalg.svd(self.Uf) # Orthogonal Weight Initialization
self.Uc = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.Uc, _, _ = np.linalg.svd(self.Uc) # Orthogonal Weight Initialization
self.Uo = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.Uo, _, _ = np.linalg.svd(self.Uo) # Orthogonal Weight Initialization
self.bi = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
self.bf = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
self.bc = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
self.bo = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
def get_grads(self):
return [self.dWi, self.dWf, self.dWc, self.dWo,
self.dUi, self.dUf, self.dUc, self.dUo,
self.dbi, self.dbf, self.dbc, self.dbo]
def get_params(self):
return [self.Wi, self.Wf, self.Wc, self.Wo,
self.Ui, self.Uf, self.Uc, self.Uo,
self.bi, self.bf, self.bc, self.bo]
def forward_prop(self, x, n_sequence):
self.x = x
self.n_sequence = n_sequence
self.h = np.zeros([self.n_sequence, self.hidden_units, 1])
self.C = np.zeros([self.n_sequence, self.hidden_units, 1])
self.i = np.zeros([self.n_sequence, self.hidden_units, 1])
self.i_p = np.zeros([self.n_sequence, self.hidden_units, 1])
self.c_h = np.zeros([self.n_sequence, self.hidden_units, 1])
self.c_h_p = np.zeros([self.n_sequence, self.hidden_units, 1])
self.f = np.zeros([self.n_sequence, self.hidden_units, 1])
self.f_p = np.zeros([self.n_sequence, self.hidden_units, 1])
self.o = np.zeros([self.n_sequence, self.hidden_units, 1])
self.o_p = np.zeros([self.n_sequence, self.hidden_units, 1])
for t in range(self.n_sequence):
if t == 0:
self.f_p[t] = np.dot(self.Wf, self.x[t]) + self.bf
self.i_p[t] = np.dot(self.Wi, self.x[t]) + self.bi
self.c_h_p[t] = np.dot(self.Wc, self.x[t]) + self.bc
self.o_p[t] = np.dot(self.Wo, self.x[t]) + self.bo
else:
self.f_p[t] = (np.dot(self.Wf, self.x[t]) + np.dot(self.Uf, self.h[t - 1]) + self.bf)
self.i_p[t] = (np.dot(self.Wi, self.x[t]) + np.dot(self.Ui, self.h[t - 1]) + self.bi)
self.c_h_p[t] = (np.dot(self.Wc, self.x[t]) + np.dot(self.Uc, self.h[t - 1]) + self.bc)
self.o_p[t] = (np.dot(self.Wo, self.x[t]) + np.dot(self.Uo, self.h[t - 1]) + self.bo)
self.f[t] = sigmoid(self.f_p[t])
self.i[t] = sigmoid(self.i_p[t])
self.c_h[t] = tanh(self.c_h_p[t])
self.o[t] = sigmoid(self.o_p[t])
self.C[t] = (
self.i[t] * self.c_h[t]
if t == 0
else self.i[t] * self.c_h[t] + self.f[t] * self.C[t - 1]
)
self.h[t] = self.o[t] * tanh(self.C[t])
if self.return_sequences == False:
return self.h[-1]
else:
return self.h
def back_prop(self, grads):
dh = np.zeros([self.n_sequence, self.hidden_units, 1])
dC = np.zeros([self.n_sequence, self.hidden_units, 1])
dx = np.zeros([self.n_sequence, self.input_units, 1])
# Compute dh and dC from time step T backward through 0.
for t in reversed(range(self.n_sequence)):
if t == self.n_sequence - 1:
if self.return_sequences == True:
dh[t] = grads[t]
else:
dh[t] = grads
dC[t] = dh[t] * self.o[t] * deriv_tanh(self.C[t])
else:
d1 = np.dot(self.Uo.T, dh[t + 1] * tanh(self.C[t + 1]) * deriv_sigmoid(self.o_p[t + 1]))
d2 = np.dot(self.Ui.T, dh[t + 1] * self.o[t + 1] * deriv_tanh(self.C[t + 1]) * self.c_h[t + 1] * deriv_sigmoid(self.i_p[t + 1]))
d3 = np.dot(self.Uc.T, dh[t + 1] * self.o[t + 1] * deriv_tanh(self.C[t + 1]) * self.i[t + 1] * deriv_tanh(self.c_h_p[t + 1]))
d4 = np.dot(self.Uf.T, dh[t + 1] * self.o[t + 1] * deriv_tanh(self.C[t + 1]) * self.C[t] * deriv_sigmoid(self.f_p[t + 1]))
dh[t] = d1 + d2 + d3 + d4
if self.return_sequences == True:
dh[t] += grads[t]
dC[t] = (dh[t] * self.o[t] * deriv_tanh(self.C[t]) + dC[t + 1] * self.f[t + 1])
# Compute the gradients from time step 0 through T.
for t in range(self.n_sequence):
_do = dh[t] * tanh(self.C[t]) * deriv_sigmoid(self.o_p[t])
self.dbo += _do
self.dWo += np.dot(_do, self.x[t].T)
if t > 0:
self.dUo += np.dot(_do, self.h[t - 1].T)
_di = dC[t] * self.c_h[t] * deriv_sigmoid(self.i_p[t])
self.dbi += _di
self.dWi += np.dot(_di, self.x[t].T)
if t > 0:
self.dUi += np.dot(_di, self.h[t - 1].T)
_dc = dC[t] * self.i[t] * deriv_tanh(self.c_h_p[t])
self.dbc += _dc
self.dWc += np.dot(_dc, self.x[t].T)
if t > 0:
self.dUc += np.dot(_dc, self.h[t - 1].T)
if t > 0:
_df = dC[t] * self.C[t - 1] * deriv_sigmoid(self.f_p[t])
self.dbf += _df
self.dWf += np.dot(_df, self.x[t].T)
self.dUf += np.dot(_df, self.h[t - 1].T)
dx[t] = (np.dot(self.Wo.T, _do) + np.dot(self.Wi.T, _di) + np.dot(self.Wc.T, _dc))
if t > 0:
dx[t] += np.dot(self.Wf.T, _df)
return dxThe back_prop() method consists of two key steps:
-
Computing hidden state gradients: This loop iterates backward through time steps, starting from the final step $T$ and ending at $0$, to calculate the gradients of the hidden and cell states at each step, denoted as $dh[t]$ and $dC[t]$.
-
Calculating parameter gradients: Based on the computed hidden state gradients, this step calculates the gradients of the model’s parameters, with respect to the hidden and cell states gradients.
[1] Create dataset.
# ============================
# Create Dataset
# ============================
n_sequence = 25
n_data = 100
n_sample = n_data - n_sequence # number of samples
sin_data = ds.create_wave(n_data, 0.05)
X, Y = ds.dataset(sin_data, n_sequence)[2] Create model.
We construct a LSTM layer followed by a dense layer. The dense layer employs a linear activation function.
# ============================
# Create Model
# ============================
input_units = 1
hidden_units = 32
output_units = 1
lstm = LSTM(input_units, hidden_units)
dense = Layers.Dense(hidden_units, output_units, linear, deriv_linear)[3] Training.
This model’s training function is identical to the neural network training functions introduced so far
def train(lstm, dense, X, Y, optimizer):
# Forward Propagation
last_h = lstm.forward_prop(X, n_sequence)
y = dense.forward_prop(last_h)
# Back Propagation Through Time
loss = np.sum((y - Y) ** 2 / 2)
dL = y - Y
grads = dense.back_prop(dL)
_ = lstm.back_prop(grads)
update_weights([dense, lstm], optimizer=optimizer)
return loss
history_loss = []
n_epochs = 200
lr = 0.0001
beta1 = 0.99
beta2 = 0.9999
optimizer = Optimizer.Adam(lr=lr, beta1=beta1, beta2=beta2)
for epoch in range(1, n_epochs + 1):
loss = 0.0
for j in range(n_sample):
loss += train(lstm, dense, X[j], Y[j], optimizer)[4] Prediction.
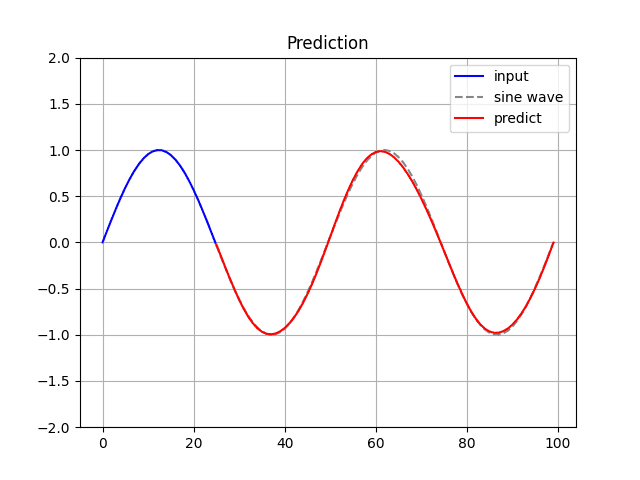
Run the following command to generate and display the predicted sine wave:
$ python LSTM_from_scratch.py
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 25, 32) 4352
dense (Dense) (None, 25, 1) 33
=================================================================
Total params: 4385
epoch: 10/200 Loss = 2.324861
epoch: 20/200 Loss = 1.085645
epoch: 30/200 Loss = 0.479348
epoch: 40/200 Loss = 0.238478
epoch: 50/200 Loss = 0.184795
epoch: 60/200 Loss = 0.168116
epoch: 70/200 Loss = 0.159275
epoch: 80/200 Loss = 0.154013
epoch: 90/200 Loss = 0.150791
epoch: 100/200 Loss = 0.148719
epoch: 110/200 Loss = 0.147262
epoch: 120/200 Loss = 0.146123
epoch: 130/200 Loss = 0.145147
epoch: 140/200 Loss = 0.144262
epoch: 150/200 Loss = 0.143434
epoch: 160/200 Loss = 0.142646
epoch: 170/200 Loss = 0.141890
epoch: 180/200 Loss = 0.141164
epoch: 190/200 Loss = 0.140462
epoch: 200/200 Loss = 0.139785