「データ構造とアルゴリズム」再入門

単方向リスト: 並行処理編 Part 2

ソースはGitHubに移行しました。

Lazy Synchronization Singly-linked List(Lazy同期 単方向リスト) pthread_mutex編

以下の論文で提案されたLazy同期リストを実装する。

S. Heller, M. Herlihy, V. Luchangco, M.Moir, W. N. Scherer III, N. Shavit,
"A Lazy Concurrent List-Based Set Algorithm",
Proc. of the Ninth International Conference on Principles of Distributed Systems, Pisa, Italy, pp.3-16, 2005

"A Lazy Concurrent List-Based Set Algorithm"

基本戦略は細粒度単方向リストの改良で、リストの走査はノードをロックせず"楽観的(Optimistic)"に"怠惰(Lazy)"に行い、 見つかったノードだけロックして走査(add/delete)する。
簡単に図示すると以下のようになる：

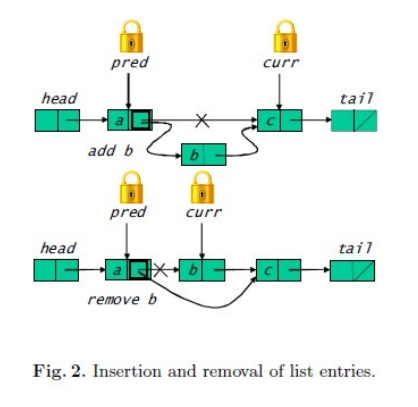
ただし、ロックをかけるタイミングによっては削除するノードの次に新ノードを追加してしまう可能性もあるので、 削除するノードにマーキングして"論理的に削除"し、追加と削除を並行実行しても不都合が起きないようにしている。
論文は擬似Javaで記述されているので、Cで再実装した。

ソースはGitHubに移行しました。

データ構造

データ構造list_tとnode_tを定義する。 list_tはListの本体、node_tはListに連結するnodeのデータ構造である。

nodeとlistのデータ構造を示す。

LazySynchroList.h:

typedef struct _node_t
{
  lkey_t key;           /* key */
  val_t val;            /* 値 */
  bool_t marked;        /* 論理的に削除されたか否かのmark */
  pthread_mutex_t mtx;  /* node毎のlock */
  struct _node_t *next; /* 次のnodeへのポインタ */
} node_t;

typedef struct _list_t
{
  node_t *head;
  node_t *tail;
} list_t;

node_tは(key,val)のペアと次のnodeへのポインタ、およびpthreadのmutex変数を保持する。 また、論理的な削除を示すbool値markedも保持する。初期値はfalseで"削除されていない"を示す。

list_tには、リストの先頭headと末尾tailが確保される。

基本関数

listの生成

/*
 * list_t *init_list(void)
 *
 * listを生成する。
 *
 * 成功すればlistへのポインタを返す。失敗ならNULLを返す。
 *
 */
list_t *init_list(void)
{
    list_t *list;

    if ((list = (list_t *) calloc(1, sizeof(list_t))) == NULL) {
      elog("calloc error");
      return NULL;
    }
    
    if ((list->head = (node_t *) calloc(1, sizeof(node_t))) == NULL) {
      elog("calloc error");
      free (list);
      goto end;
    }
    list->head->mtx = (pthread_mutex_t) PTHREAD_MUTEX_INITIALIZER;
    
    if ((list->tail = (node_t *) calloc(1, sizeof(node_t))) == NULL) {
      elog("calloc error");
      goto end;
    }
    list->tail->mtx = (pthread_mutex_t) PTHREAD_MUTEX_INITIALIZER;
    
    list->head->next = list->tail;
    list->tail->next = NULL;
  
  return list;

 end :
  free (list->head);
  free (list);
  return NULL;
}

ノードの追加

ノードの追加を行う関数add()を示す。
基本戦略はノードの走査は「楽観的に」ロックをかけずに行い、 目的のノード(追加手前のノードpredとその次のノードsucc)を見つけた後にロックする。 それから新しいノードnewNodeをpredとsuccの間に追加する。
なお、マクロ validateはdelete()のアルゴリズムを見ると理解しやすいので ここでは詳細を省き、「削除対象でないことを保証するマクロ」とだけ記す。

/*
 * bool_t add(list_t * list, const lkey_t key, const val_t val)
 *
 * listにnode(key,val)を追加する。
 * 追加位置はkeyの昇順に従う。すでに同じkeyを持つnodeがある場合は失敗。
 *
 * 成功すればtrue、失敗すればfalseを返す。
 */
#define validate(pred, curr) (!pred->marked && !curr->marked && pred->next == curr)

bool_t add(list_t * l, const lkey_t key, const val_t val)
{
    node_t *pred, *curr;
    node_t *newNode;
    bool_t ret = true;

    if ((newNode = create_node(key, val)) == NULL)
      return false;

    while (1) {
      pred = l->head;
      curr = pred->next;
      
      /* 目的のノードまで走査 */	
      while (curr->key < key && curr != l->tail) {
	pred = curr;
	curr = pred->next;
      }
      
      /* 
       * この間に、他のスレッドがpredやcurrを削除、変更、または
       * ノードを追加する可能性がある
       */
      
      if (lock(&pred->mtx) != 0) {      /* lockが成功しなければ、最初からやりなおし */	
	continue;
      } else if (lock(&curr->mtx) != 0) {
	unlock(&pred->mtx);
	continue;
      }
      /* この時点で成立する条件式: (pred->key) < (newNode->key) <= (curr->key) */
      assert ((pred->key < key) && (key <= curr->key));
      
      /* クリティカルセクション開始 */
      if (validate(pred, curr)) {
	if (key == curr->key) {
	  ret = false;
	  free_node(newNode);
	} else {
	  newNode->next = curr;
	  pred->next = newNode;
	}
	/* クリティカルセクション終了 */
	unlock(&pred->mtx);	unlock(&curr->mtx);
	break;
      }
      unlock(&pred->mtx);      unlock(&curr->mtx);
    }
    return ret;
}

関数add()内部で呼ぶnode生成関数create_node()を示す。

/*
 * node_t *create_node(const lkey_t key, const val_t val)
 *
 * (key, val)を持つnodeを生成する。
 *
 * 成功すればnodeへのポインタを返す。失敗すればNULLを返す。
 */
static node_t *create_node(const lkey_t key, const val_t val)
{
    node_t *node;

    if ((node = calloc(1, sizeof(node_t))) == NULL) {
      elog("calloc error");
      return NULL;
    }
    node->mtx = (pthread_mutex_t) PTHREAD_MUTEX_INITIALIZER;

    node->key = key;
    node->val = val;

    return node;
}

ノードの削除

ノードの削除も基本戦略は追加と同じである。よって実装にも上と同じ問題を抱えている。
ノードの属性:markedは、ロックした後にfalseからtrueに変更される。これにより論理的に削除されたことになる。 次に実際にfreeでメモリ領域が開放され物理的にも削除される。

/*
 * bool_t delete(list_t * list, const lkey_t key, val_t *val)
 *
 * listからkeyを持つnodeを削除し、そのnodeのvalを*valに書き込む。
 * keyが存在しない場合は失敗。
 *
 * 成功すればtrue、失敗すればfalseを返す。
 */
#define validate(pred, curr) (!pred->marked && !curr->marked && pred->next == curr)

bool_t delete(list_t * l, const lkey_t key, val_t *val)
{
  node_t *pred, *curr;
  bool_t ret = true;
  
  while(1) {
    pred = l->head;
    curr = pred->next;
    
    if (curr == l->tail) {
      ret = false;
      break;
    } else {
      /* 目的のノードまで走査 */
      while (curr->key < key && curr != l->tail) { 
	pred = curr;
	curr = pred->next;
      }
      
      /* 
       * この間に、他のスレッドがpredやcurrを削除、変更、または
       * ノードを追加する可能性がある
       */
      
      if (lock(&pred->mtx) != 0) {	/* lockが成功しなければ、最初からやりなおし */
	continue;
      } else if (lock(&curr->mtx) != 0) {
	unlock(&pred->mtx);
	continue;
      }

      /* この時点で成立する条件式: (pred->key) < (newNode->key) <= (curr->key) */
      assert ((pred->key < key) && (key <= curr->key));
      
      /* クリティカルセクション開始 */
      if (validate(pred, curr)) { 
	if (key == curr->key) {
	  curr->marked = true;
	  *val = curr->val;
	  pred->next = curr->next;
	  free_node(curr);
	} else {
	  ret = false;
	}
	/* クリティカルセクション終了 */
	unlock(&pred->mtx);	unlock(&curr->mtx);
	break;
      }
      unlock(&pred->mtx);      unlock(&curr->mtx);
    }
  }
  return ret;
}

ノードの検索

/*
 * bool_t find(list_t * list, const lkey_t key, val_t *val)
 *
 * listからkeyを持つnodeを検索し、そのnodeのvalを*valに書き込む。
 * keyが存在しない場合は失敗。
 *
 * 成功すればtrue、失敗すればfalseを返す。
 */
bool_t find(const list_t * list, const lkey_t key)
{

    node_t *curr;

    curr = list->head;
    while (curr->key < key) {
	curr = curr->next;
    }
    
    return (curr->key == key && !curr->marked);
}

実行

ソースはGitHubに移行しました。

---

---